- 정의
황금분할 ( 黃金分割 : Golden Section )
선분을 한 점에 의하여 2개의 부분으로 나누어, 그 한쪽의 제곱을, 나머지와 전체와의 곱과 같아지게 하는 일.
하나의 선분 AB가 있을 때, 그 선분상에 한 점 P를 구하여 (AP)·(AP) = (BP)·(AB) 가 되도록 하는 일이다.
" (BP) : (AP) = 1:0.61803… " 을 황금비(黃金比) 또는 외중비(外中比)라 한다.
황금비는 고대 그리스에서 발견되었고, 가장 조화가 잡힌 비(比)로서 이와 같이 이름하게 된 것인데,
르네상스의 볼로냐의 수도승(修道僧) 루카 바티리오에 의하여 ‘신성비례(神聖比例)’라고 이름할 정도로 중요시되었다.
특히 시각(視覺)에 호소하는 도형이나 입체 등에서는 이 비를 많이 이용해 왔으며, 예를 들면 직사 각형의 두 변의 비가
황금분할이 되는 것은 여러 가지 비례의 직사각형 중에서 가장 정돈된 직사각형이라 하였다.
건축·조각·회화·공예(工藝) 등, 조형예술의 분야에서는 다양한 통일의 하나의 원리로서 널리 활용되고 있다.
또, 자연의 조화가 잡힌 형태 중, 예를 들면 잎맥[葉脈], 종자의 형상, 조개껍데기 소용돌이, 세 포의 성장 등에서 이 비를
찾아내려고 하는 사람도 있다.
근년에는 음악 영역에서도 이것을 작곡에 활용한 예가 있다.
황금비는 일상 생활 속에서도 쉽게 찾을 수 있다.
예를 들면 엽서, 담배갑이나 명함의 치수 등도 두 변의 비가 황금비에 가깝다.
물건을 선택할 때 대부분의 사람은 무의식 중에 황금비의 치수를 취하고 있다.
피보나치의 수열에서 5를 A라 하고 8을 B라 하자. 5/8은 0.6에 가깝고 또 8/ 13(=5+8)도 역시 0.6이 된다. 반대로 8을 5로, 13을 8로 나누면 1.6이 된다. 등식의 형태로 나타내면 A:B=B:(A+B)가 되며 이것이 바로 황금분할 또는 황금비율의 등식이며 일반적으로 황금비율을 말할 때는 0.618 또는 1.618을 의미한다. 어떤 주어진 선이 있다고 하자. 이 직선 상에서 A:B=B:(A+B)의 등식이 충족되게 나눌 수 있는 점은 오직 한 점이며 이 점을 황금분할의 점(전체의 61.8%에 해당하는 점)이라 한다.(그림1 참조)
그러므로 황금분할이라 함은 전체 속에서 두 개의 크기가 다른 부분 사이의 독특한 상호관계이며 황금분할이란 용어는 이 비율관계의 절묘함에서 나온 말이다.
인간의 시각에서 볼 때 파이(Ø, 1.618)의 비율을 응용하여 만든 물건, 건축물 등은 다른 비율을 사용해 만든 것에 비해 가장 안정적으로 느껴진다. 꽃의 꽃잎 속에서도 파이의 비율을 발견할 수 있으며 우리가 느끼는 아름다운 화음에서도 이 비율이 적용된다고 한다. 심지어 우리가 일반적으로 볼 때 아름답다고 느껴지는 몸매를 가진 팔등신의 여인들도 확인해 보면 그들의 몸 전체에서 배꼽의 위치가 발바닥에서부터 정확히 몸 전체의 61.8%에 해당된다. 더불어 주식시장에서도 황금분할의 법칙에 의해 행동하는 인간의 행태가 나타난다. 파이가 인간에게 호감과 조화감을 준다는 사실은 고대부터 인정된 사실이었으며 지난 세기말 이래로 많은 과학적 실험으로도 증명되어 왔다.
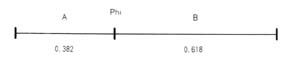
그렇다면 왜 파이가 인간에게 호감과 조화감을 줄까? 그 이유는 아직 과학적으로 정확히 설명이 안되고 있다. 일부 사람들은 이런 숨겨진 현상을 자연적인 우연이라고 믿고 싶을 수도 있을 것이다. 그러나 이러한 우연이 규칙성을 갖고 반복한다면 그 우연은 평범한 우연이 아닐 것이다. 분명히 파이는 인간의 심리에 영향을 미치는 보이지 않는 질서가 있다. 이러한 인식은 ‘모든 것의 근원은 수’라고 생각했던 고대 피타고라스 학파의 사람들에게는 경이적인 당연한 사실로 받아들여졌으며 파이(61.8%) 안에서 우주질서의 비밀을 느꼈다. 그들은 파이를 단순한 숫자로 생각하기 보다는 신성한 하나의 상징으로 인식했고 파이로 말미암아 숫자의 신비스러움에 대한 그들의 신뢰를 높여 주었다. 그러기에 그들은 황금분할의 비율이 내재된 오각형 별(그림 2)을 피타고라스 학파의 상징으로 삼고 자신의 특성을 보존하면서 전체의 더 큰 형태에 융화되는 황금분할의 특징처럼 구성원들이 모든 사치를 금하고 검소한 생활을 하며 사회적으로 의료시술 등의 봉사활동을 하는 등 전체사회 구성원으로서 자신의 위치를 조화시켜 나갔다.
- 정리
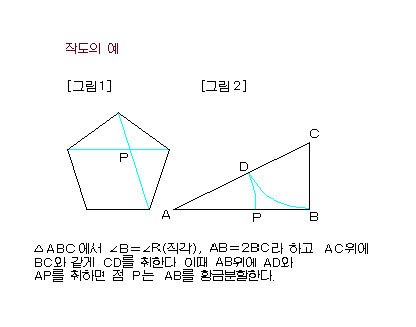
피보나치의 수열에서 5를 A라 하고 8을 B라 하자. 5/8은 0.6에 가깝고 또 8/ 13(=5+8)도 역시 0.6이 된다. 반대로 8을 5로, 13을 8로 나누면 1.6이 된다. 등식의 형태로 나타내면 A:B=B:(A+B)가 되며 이것이 바로 황금분할 또는 황금비율의 등식이며 일반적으로 황금비율을 말할 때는 0.618 또는 1.618을 의미한다. 어떤 주어진 선이 있다고 하자. 이 직선 상에서 A:B=B:(A+B)의 등식이 충족되게 나눌 수 있는 점은 오직 한 점이며 이 점을 황금분할의 점(전체의 61.8%에 해당하는 점)이라 한다.(그림1 참조)
그러므로 황금분할이라 함은 전체 속에서 두 개의 크기가 다른 부분 사이의 독특한 상호관계이며 황금분할이란 용어는 이 비율관계의 절묘함에서 나온 말이다.
인간의 시각에서 볼 때 파이(Ø, 1.618)의 비율을 응용하여 만든 물건, 건축물 등은 다른 비율을 사용해 만든 것에 비해 가장 안정적으로 느껴진다. 꽃의 꽃잎 속에서도 파이의 비율을 발견할 수 있으며 우리가 느끼는 아름다운 화음에서도 이 비율이 적용된다고 한다. 심지어 우리가 일반적으로 볼 때 아름답다고 느껴지는 몸매를 가진 팔등신의 여인들도 확인해 보면 그들의 몸 전체에서 배꼽의 위치가 발바닥에서부터 정확히 몸 전체의 61.8%에 해당된다. 더불어 주식시장에서도 황금분할의 법칙에 의해 행동하는 인간의 행태가 나타난다. 파이가 인간에게 호감과 조화감을 준다는 사실은 고대부터 인정된 사실이었으며 지난 세기말 이래로 많은 과학적 실험으로도 증명되어 왔다.
그렇다면 왜 파이가 인간에게 호감과 조화감을 줄까? 그 이유는 아직 과학적으로 정확히 설명이 안되고 있다. 일부 사람들은 이런 숨겨진 현상을 자연적인 우연이라고 믿고 싶을 수도 있을 것이다. 그러나 이러한 우연이 규칙성을 갖고 반복한다면 그 우연은 평범한 우연이 아닐 것이다. 분명히 파이는 인간의 심리에 영향을 미치는 보이지 않는 질서가 있다. 이러한 인식은 ‘모든 것의 근원은 수’라고 생각했던 고대 피타고라스 학파의 사람들에게는 경이적인 당연한 사실로 받아들여졌으며 파이(61.8%) 안에서 우주질서의 비밀을 느꼈다. 그들은 파이를 단순한 숫자로 생각하기 보다는 신성한 하나의 상징으로 인식했고 파이로 말미암아 숫자의 신비스러움에 대한 그들의 신뢰를 높여 주었다. 그러기에 그들은 황금분할의 비율이 내재된 오각형 별(그림 2)을 피타고라스 학파의 상징으로 삼고 자신의 특성을 보존하면서 전체의 더 큰 형태에 융화되는 황금분할의 특징처럼 구성원들이 모든 사치를 금하고 검소한 생활을 하며 사회적으로 의료시술 등의 봉사활동을 하는 등 전체사회 구성원으로서 자신의 위치를 조화시켜 나갔다.
- 황금분할의 구도가 내재된 직사각형
황금분할이 나타내는 현상과 그 의미하는 것을 이해하려면 황금분할 구도가 내재된 직사각형을 이해하여야 한다.
황금분할의 구도가 내재된 직사각형은 다음과 같은 방법으로 구할 수 있다.
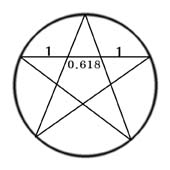
첫째 그림3과 같이 길이가 각각 2단위의 정사각형 ABCD를 작성한 후 밑변 CD의 중간지점을 E라고 정하고 BE를 이으면 밑변 1, 높이 2인 직각삼각형 BCE가 형성된다.
삼각형 BCE의 빗변 BE의 길이는 ‘빗변의 곱은 다른 두변의 각각의 제곱의 합과 일치한다’는 피타고라스의 정리에 의해 √ 5 단위의 길이를 갖게 된다. 다음 단계는 그림3 같이 EG의 길이가 삼각형의 빗변 BE의 길이 √ 5 와 같도록 연장한다. 모두 완성이 되면 (그림 3)에서는 다음과 같은 황금분할의 관계가 형성된다.
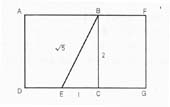
FG=2 FG=2
DG/FG = (√ 5 +1)/2 CG/FG = (√ 5 -1)/2
= (2.236+1)/2 = (2.236-1)/2
= 3.236/2 = 1.236/2
= 1.618 = 0.618
위 두 식의 답은 모두 황금분할의 수 파이(Ø) 1.618과 0.618임을 알 수 있으며 직사각형 ADGF를 ‘황금직사각형(Golden Rectangle)’이라 말하며 직사각형 BCGF도 역시 ‘황금직사각형’이다.
한 변의 길이가 1인 정5각형 abcde에서
△ ACD ∽ △ CDF
∵ ∠ ADC = ∠ ADB + ∠ BDC
= ∠ ADB + ∠ BEC
= ∠ CAF + ∠ CAF
= ∠ CFD
또 ∠ ACD = ∠ ADC
따라서
선분AC : 선분CD = 선분CD : 선분FD
x : 1 = 1 : (x - 1)
∴ x = (1 + root{5})/2 (황금비)
FG=2 FG=2
DG/FG = (√ 5 +1)/2 CG/FG = (√ 5 -1)/2
= (2.236+1)/2 = (2.236-1)/2
= 3.236/2 = 1.236/2
= 1.618 = 0.618
위 두 식의 답은 모두 황금분할의 수 파이(Ø) 1.618과 0.618임을 알 수 있으며 직사각형 ADGF를 ‘황금직사각형(Golden Rectangle)’이라 말하며 직사각형 BCGF도 역시 ‘황금직사각형’이다.
한 변의 길이가 1인 정5각형 abcde에서
△ ACD ∽ △ CDF
∵ ∠ ADC = ∠ ADB + ∠ BDC
= ∠ ADB + ∠ BEC
= ∠ CAF + ∠ CAF
= ∠ CFD
또 ∠ ACD = ∠ ADC
따라서
선분AC : 선분CD = 선분CD : 선분FD
x : 1 = 1 : (x - 1)
∴ x = (1 + root{5})/2 (황금비)
- 황금나선구조
황금분할의 구조는 인간이 만든 특정 조형물이나 자연의 주어진 정적인 상태에 대한 심미적 분석에 유용하나 동적인 상태의 분석에는 한계가 있다.
자연의 동적인 상태, 즉 성장, 발전, 진행 등을 황금분할의 관점에서 분석하기 위해서는 황금나선구조의 이해가 필수적이다.
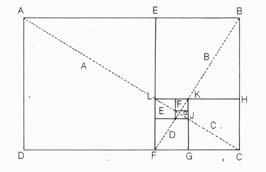
이러한 정사각형들 A, B, C, D, E, F … 등으로의 진행은 이론적으로는 점 Q를 향해 무한소로 진행되어 갈 수 있으며 각각의 사각형들은 서로 황금분할로 분할되어 있다.
그 예로 정사각형 A는 전체 사각형의 나머지 부분(사각형 EBCF)과 황금분할을 이루고 있고 정사각형 B는 사각형 HCFL과 황금분할을 이루고 있다. 황금분할을 내재한 직사각형의 Q를 중심으로 각 정사각형에 내재한 1/4원(호)을 그려 나가면 그림8과 같은 나선형구조의 호들이 연결된 형태를 보여줄 것이다. 이 호들의 연결된 형태를 황금나선(Golden Spiral)이라 하며 그 진행은 무한대로 뻗어나갈 수 있다. 이 황금나선의 연결된 각 호들의 상호비율을 측정해 보면 황금비율을 내재하고 있는 사실을 쉽게 알 수 있다.
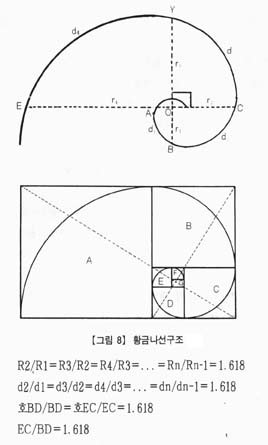
위의 식들에서 나타난 것 같이 황금나선의 X축, Y축을 기준으로 한 각각의 호와 그 반지름은 1.618의 비율로 커나감을 볼 수 있다. 또한 황금나선은 중심을 향해 무한소로 수축되며 동시에 무한대로 팽창해 나감을 알 수 있다. 변형되지 않는 일정한 비율(1.618)을 유지하며 무한대로 팽창하는 황금나선의 특징은 다른 어느 모형에서도 찾아볼 수 없는 독특한 것이며 고대 이집트인들의 사후세계의 개념(일정하게 팽창하는 무한정의 공간과 무한대의 시간)과 일치하는 것으로 이집트인들은 황금나선의 황금비율을 피라미드 건축시 중요한 기준으로 삼았다.
20세기 미국의 철학자 홀은 “우주의 모든 것은 생명이 있고, 그것들은 끝없이 생장, 팽창하며 그 기준과 규칙은 황금비율이다. 따라서 황금비율이야말로 신의 형태를 드러내주는 현상적 기준이다.”라고 말했다.
고대 그리스 수학의 대명사인 피타고라스는 자신이 세운 학교의 상징을 황금비율에 의해 그려진 별모양으로 삼았으며 자화상의 오른손에 피라미드(황금분할이 적용된 극명한 예)를 그려넣고 ‘우주의 비밀(The Secret of the Universe)’이라는 문장을 새겨 넣었다. 그는 그렇게 함으로써 황금분할이 우주의 비밀을 푸는 열쇠라는 사실을 보여주려 했으며 황금분할의 발견을 그의 인생에 있어서 가장 큰 업적으로 남기려 했음을 볼 수 있다.
또한 우주 운행의 질서를 지배하는 메카니즘을 밝혀 물리학의 새로운 지평을 연 아이작 뉴턴은 황금나선구조를 자신의 침대 머리맡에 새겨놓았다.
뉴턴 물리학의 기본 패러다임은 ‘결정론적 인과율’이다. 모든 운동의 원인이 되는 초기 조건만 정확히 알면 그 결과는 뉴턴의 선형 이분 방정식에 의해서 기계적으로, 다시 말해 필연적으로 얻어진다는 것이다. 이는 바로 황금나선구조의 이론 그 자체인 것이다.
우주에 존재하는 모든 것은 성장형태(form)가 있고 내재된 질서가 있다. 우주의 영문어원 자체도 uni(one) + verse(order) = one order 즉 하나의 질서를 의미한다. 우주의 모든 것은 성장형태가 있고 그것들의 기준 중의 하나가 황금분할이라는 가정이 사실이라면, 끝없이 생장하며 지구상에서 다수의 인간집단들이 동시에 참여하며 각각의 행위가 집단적 행위의 결과로 이어지는 주식시장에서도 황금분할의 법칙이 적용되어야 할 것이 아니겠는가라고 생각한 것이 엘리오트이다. 이 세상의 모든 것들은 단속(斷續)적인 시공(時空)이 아닌, 연속(連續)적인 시공(時空)에 존재하기 때문에 과거의 행위는 어떤 형태로든지 미래의 결과에 영향을 미친다.
엘리오트는 그의 두 번째 저서 ‘자연의 법칙(부제:우주의 비밀)-Nature’s Law <the Secret of the Universe>’에서 황금분할의 법칙에 근거한 그의 파동이론을 생물, 수학, 미술, 심리학 그외 인간행동의 모든 분야에 적용해 보았다.
엘리오트는 자신의 이론을 확신한 나머지 그의 이론을 여러 분야에 걸쳐 적용시켜 보았으나 결코 그의 이론만으로 이 세상의 수많은 형태와 질서를 설명하기에는 무리가 있었다. 그러나 분명한 것은 엘리오트의 파동이론은 우주를 지배하는 중요한 질서 중의 하나의 흐름을 주식시장에까지 적용하여서 성공적이기도 하였다는 것이다.
출처: http://knot.kaist.ac.kr/~trefoil/hs100/golden/in.html
'자료 #00: 나머지' 카테고리의 다른 글
| 화공기사 실기 2014년 1회 필답 (0) | 2018.04.13 |
|---|---|
| 화공기사 실기 2013년 4회 필답 (0) | 2018.04.12 |
| 화공기사 자격 취득 도우미 (0) | 2018.04.12 |
| 화공기사 실기 2016년 2회 필답 (0) | 2018.04.12 |
| 화공기사 실기 2017년 1회 필답 (0) | 2018.04.12 |
| 화공기사 실기 2015년 2회 필답 (0) | 2018.04.10 |
| 화공기사 실기 2016년 1회 필답 (0) | 2018.03.22 |
| 지식인으로 가게 이름 짓기 (0) | 2011.12.26 |